Machine Learning Part 1: Introduction

My goal with this (planned) series of blog posts is to explain and derive the fundamental algorithms of machine learning. This includes linear regression and classification techniques, as well as some non-linear methods such as neural networks and support vector machines. My hope is that these posts serve to both solidify my own knowledge on the topic, as well as being notes that I can refer to in the future.

Defining Machine Learning

Artificial intelligence describes the ability of machines to think and make decisions (or predictions) in a rational, and human-like way. Machine learning is a subset of artificial intelligence where decision-making is based on data and a statistical model. The goal is to develop a statistical model from a given dataset. We can then use this statistical model to make predictions on new and different data. This type of learning is similar to experential learning; a learning method where patterns are developed from past experiences.

Machine Learning Model

Developing a machine learning model can be split into two major steps:

1. learning / training
2. prediction / inference

The training stage involves developing a model by applying a machine learning algorithm to a dataset.

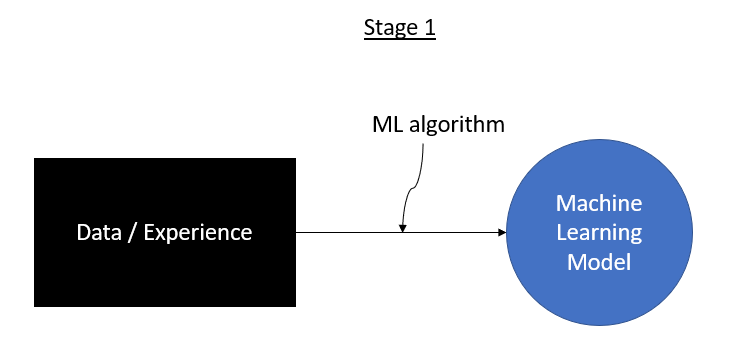
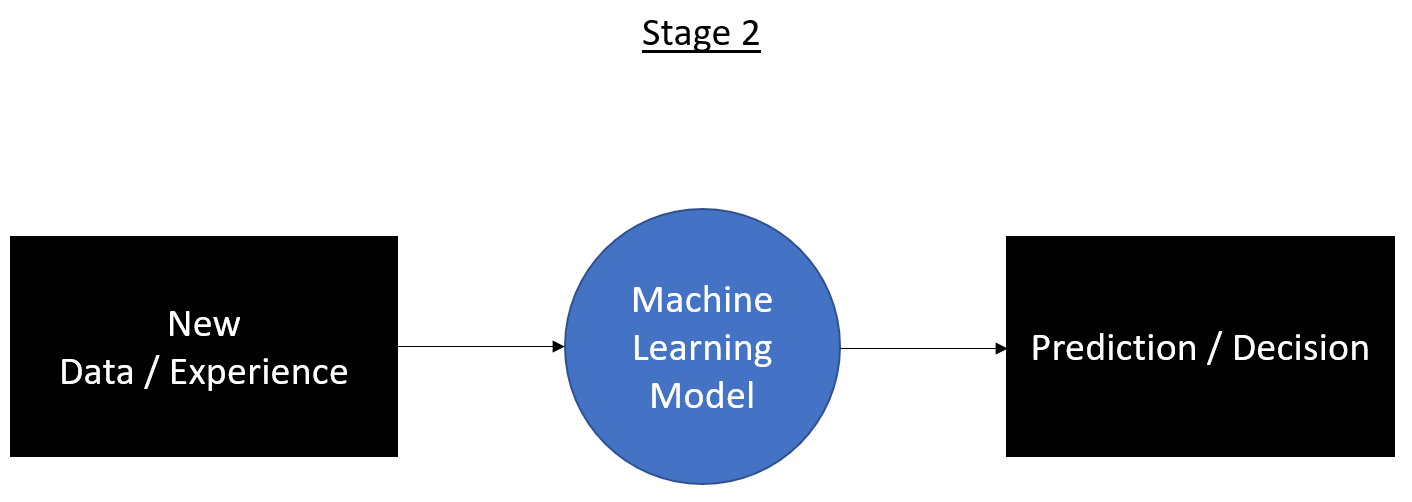
The prediction stage involves taking new data and using our developed machine learning model to make a prediction.

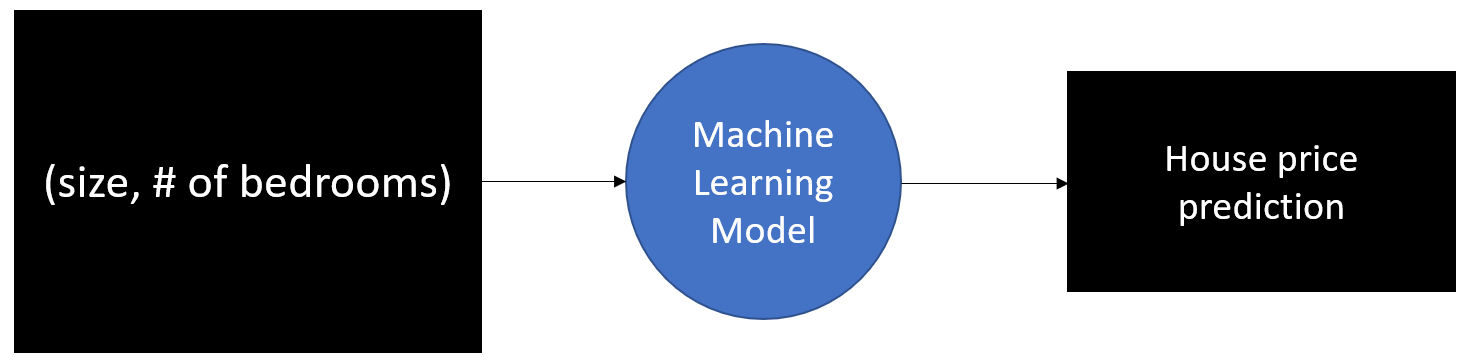
Let's say we want to build a machine learning model to predict house prices. We have data on a bunch of other houses such as their associated house price along with properties of the house such as its size and number of bedrooms.

size	# of bedrooms	price
2960	4	640,000
1740	3	990,000
3100	5	780,000
...	...	...

We want to use an algorithm that finds a relationship between the price of a home and its size and number of bedrooms. We use the above data (training data) along with our algorithm to build a model that predicts the price of a house given its size and number of bedrooms (stage 1). For stage 2, we take the size and number of bedrooms of the new houses we want to predict the price for, and feed the data into our model to make a prediction.

Categories of Machine Learning

There are 3 main categories of machine learning:

1. Supervised Learning
2. Unsupervised Learning
3. Reinforcement Learning

The task of predicting house prices is an example of supervised learning. We have a specific goal of prediction which we are aware of during the training stage. In supervised learning, our data has "features" (ex: size, # of bedrooms) along with the "correct" answer produced from the features (ex: house price). We'll discuss supervised learning in more detail below. In unsupervised learning, we don't have a specific goal of prediction. Our training data doesn't have a correct answer and we try to find relationships among the features. Reinforcement learning is a way to make decisions based on a reward system where we have an agent that tries to obtain the maximum reward. I'll mainly be focusing on supervised learning.

Supervised Learning

In a previous section, we went over the two major steps of machine learning. In the first step, we have the learning / training phase where we train a model based off our training data. We can think of this stage as the studying stage where the training data is like our homework. Once our homework is marked, we receive a score on how well we did. The goal of this stage is to receive the highest mark or to minimize the amount of wrong answers. Doing our homework allows us to learn the material and potentially generalize our knowledge to other problems. Seeing how well we can generalize our knowledge to other problems is akin to writing a test. That's the point of the prediction step, we take what we learned from the training data and apply it to brand new problems and see how good our model does.

The machine learning model is essentially a function, $f$, that takes input data and maps it to an output. In regression, the output of $f$ will be a continuous number like house price or salary. In classification, the output of $f$ will be a discrete value such as dog, cat, mouse, or some other type of categorical output. Our training data can be subdivided into its features and response variables.

$\mathbf{x}$ is a vector of features (ex: size, # of bedrooms) and $y$ is the response (ex: house price). $M$ is the number of samples (or rows) we have in our dataset. The entries in vector $\mathbf{x}^{m}$ represent the value for each corresponding feature. We use a machine learning algorithm to learn a function $f$ from the training data. What does it mean to learn a function? Unfortunately, a function doesn't just magically appear out of thin air. We have to hypothesize functions ourselves which we think might fit the data. Examples of functions include linear functions, quadratics, sinusoids, and much more. In a linear function, $y = mx + b$, we have to specify the values for the slope, $m$, and the y-intercept $b$. How do we know which values of $m$ and $b$ result in the best fit? We first need to specify a loss function, $J$, to determine how close our prediction is to the actual true value.

The above is an example of a common loss function. It is essentially finding the squared error for each prediction ($f(x^{(m)})$) versus its true value. Our goal is to minimize the loss function so that we end up with the smallest error. When using a linear function, we try to find the optimal values for $m$ and $b$. The optimal values are the values that result in $J$ being at its minimum.

We then evaluate our trained model, $f$, on a different dataset called the test set.

The test features, $\mathbf{x}_{*}$, are fed into our model, $f$, which outputs a predicted value $\hat{y}$ (same as $f(x)$). How do we evaluate the performance of our model i.e. how well did it do at predicting a certain value such as house prices? There are many different measures to evaluate our model including Mean-Squared Error (MSE), Mean Absolute Percentage Error (MAPE), and more. The aforementioned measures of accuracy all use different equations to compare our prediction, $\hat{y}$, with the true value, $y_{*}$. Choosing a measure of success depends on the task.